OPERADORES O EXPRESIONES

Las expresiones u operadores son combinaciones de constantes, variables, símbolos de operación, paréntesis y nombres de funciones especiales. 

Cada expresión toma un valor que se determina tomando los valores de las variables y constantes implicadas y la ejecución de las operaciones indicadas. Una expresión consta de operandos y operadores. Según sea el tipo de objetos que manipulan, las expresiones se clasifican en: 

• aritméticas,
• relacionales, 
• lógicas, 
• carácter. 

El resultado de la expresión aritmética es de tipo numérico; el resultado de la expresión relacional y de una expresión lógica es de tipo lógico; el resultado de una expresión carácter es de tipo carácter.

EXPRESIONES ARITMÉTICAS

Las expresiones aritméticas son análogas a las fórmulas matemáticas. Las variables y constantes son numéricas (real o entera) y las operaciones son las aritméticas.

•  +   suma 
• -   resta 
• *   multiplicación 
• /   división 
• ↑, **, ^   exponenciación 
• div, /   división entera
• mod, %   módulo (resto) 

Los símbolos +, –, *, ^ (↑ o **) y las palabras clave div y mod se conocen como operadores aritméticos. En la expresión 5 + 3 los valores 5 y 3 se denominan operandos. El valor de la expresión 5 + 3 se conoce como resultado de la expresión. Los operadores se utilizan de igual forma que en matemáticas. Por consiguiente, A ∙ B se escribe en un algoritmo como A * B y 1/4 ∙ C como C/4. Al igual que en matemáticas el signo menos juega un doble papel, como resta en A – B y como negación en –A.

Reglas de prioridad

Las expresiones que tienen dos o más operandos requieren unas reglas matemáticas que permitan determinar el orden de las operaciones, se denominan reglas de prioridad o precedencia y son: 

1. Las operaciones que están encerradas entre paréntesis se evalúan primero. Si existen diferentes paréntesis anidados (interiores unos a otros), las expresiones más internas se evalúan primero. 

2. Las operaciones aritméticas dentro de una expresión suelen seguir el siguiente orden de prioridad: 

• operador ( ) 
• operadores ++, – – + y – unitarios, 
• operadores *, /, % (producto, división, módulo) 
• operadores +, – (suma y resta). 

En los lenguajes que soportan la operación de exponenciación, este operador tiene la mayor prioridad. En caso de coincidir varios operadores de igual prioridad en una expresión o subexpresión encerrada entre paréntesis, el orden de prioridad en este caso es de izquierda a derecha, y a esta propiedad se denomina asociatividad

Conclusión:

En mi opinión, todas estas son una pieza clave a la hora del desarrollo de diferentes diagramas de flujo e incluso en el ámbito de la programación. No obstante, también creo que esto es algo que cualquiera que quiera estudiar algo relacionado con la programación, o vaya, el software debería de saber de ante mano para así tener más facilidad en las diferentes actividades que te puedan surgir.

EXPRESIONES DE RELACIÓN

 Los operadores relacionales o de relación permiten realizar comparaciones de valores de tipo numérico o carácter. Los operadores de relación sirven para expresar las condiciones en los algoritmos.

 Operadores de relación:

Operador   Significado 

<                 menor que

 >                mayor que

 =, ==          igual que

 <=             menor o igual que

 >=             mayor o igual que 

<>, !=          distinto de 

 Los operadores de relación se pueden aplicar a cualquiera de los cuatro tipos de datos estándar: enteros, real, lógico, carácter. La aplicación a valores numéricos es evidente. Los ejemplos siguientes son significativos: 

Para realizar comparaciones de datos tipo carácter, se requiere una secuencia de ordenación de los caracteres similar al orden creciente o decreciente. Esta ordenación suele ser alfabética, tanto mayúsculas como minúsculas, y numérica, considerándolas de modo independiente. Pero si se consideran caracteres mixtos, se debe recurrir a un código normalizado como es el ASCII. Aunque no todas las computadoras siguen el código normalizado en su juego completo de caracteres, sí son prácticamente estándar los códigos de los caracteres alfanuméricos más usuales. Estos códigos normalizados son: 

• Los caracteres especiales #, %, $, (, ), +, –, /, ..., exigen la consulta del código de ordenación. 
• Los valores de los caracteres que representan a los dígitos están en su orden natural. Esto es, '0'<'1', '1'<'2', ..., '8'<'9'. 
• Las letras mayúsculas A a Z siguen el orden alfabético ('A'<'B', 'C'<'F', etc.). 
• Si existen letras minúsculas, éstas siguen el mismo criterio alfabético ('a'<'b', 'c'<'h', etc.). 

En general, los cuatro grupos anteriores están situados en el código ASCII en orden creciente. Así, '1'<'A' y 'B'<'C'. Sin embargo, para tener completa seguridad será preciso consultar el código de caracteres de su computadora (normalmente, el ASCII, American Standar Code for Information Interchange o bien el ambiguo código EBCDIC, Extended Binary-Coded Decimal Interchange Code, utilizado en computadoras IBM diferentes a los modelos PC y PS/2).

 Cuando se utilizan los operadores de relación, con valores lógicos, la constante false (falsa) es menor que la constante true (verdadera). 

false < true 

true > false

Si se utilizan los operadores relacionales = y <> para comparar cantidades numéricas, es importante recordar que la mayoría de los valores reales no pueden ser almacenados exactamente. En consecuencia, las expresiones lógicas formales con comparación de cantidades reales con (=), a veces se evalúan como falsas, incluso aunque estas cantidades sean algebraicamente iguales.

Conclusión:
La mayoría de los operadores anteriores son conocidos por la mayoría de personas, no obstante, muy pocas saben el orden y la forma correcta de utilizar estos para la programación eficaz y rápida la cual es utilizada en la mayoría de aparatos electronicos, moviles que utilizamos en nuestro día a día.

EXPRESIONES LÓGICAS

Los operadores lógicos o booleanos básicos son not (no), and (y) y or (o).


Las definiciones de las operaciones no, y, o se resumen en unas tablas conocidas como tablas de verdad.


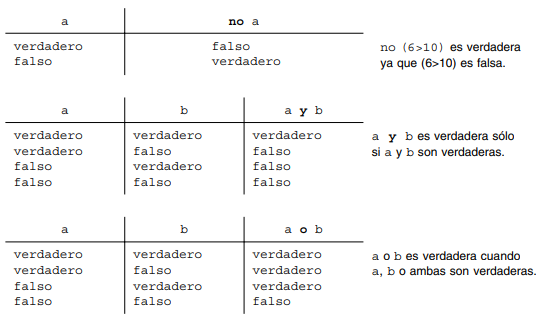
 En las expresiones lógicas se pueden mezclar operadores de relación y lógicos. Así, por ejemplo,
(1 < 5) y (5 < 10) es verdadera (5 > 10) o ('A' < 'B') es verdadera, ya que 'A' < 'B'

Conclusión:
Se dan a conocer los punto más básicos de estos operadores los cuales seran una parte fundamental de la programación de programas informáticos complejos.

Prioridad de los operadores
Los operadores aritméticos seguían un orden específico de prioridad cuando existía más de un operador en las expresiones. De modo similar, los operadores lógicos y relaciones tienen un orden de prioridad.
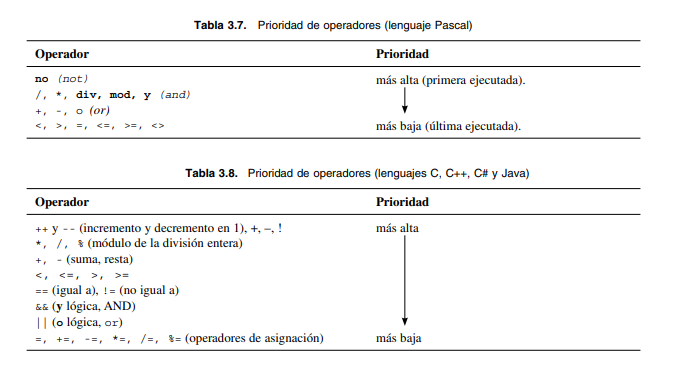Al igual que en las expresiones aritméticas, los paréntesis se pueden utilizar y tendrán prioridad sobre cualquier operación. 

Conclusión:
La gran variedad de lenguajes de programación hacen que la prioridad vaya variando dependiendo de aquel lenguaje que utilizemos o sea necesario.





Fuentes consultadas:

Luis Joyanes Aguilar. FUNDAMENTOS DE PROGRAMACIÓN Algoritmos, estructura de datos y objetos (Cuarta edición). Obtenida el 29 de agosto del 2019, de: http://combomix.net/wp-content/uploads/2017/03/Fundamentos-de-programaci%C3%B3n-4ta-Edici%C3%B3n-Luis-Joyanes-Aguilar-2.pdf